Knotwork Tutoroial-Alternative Grids

1.

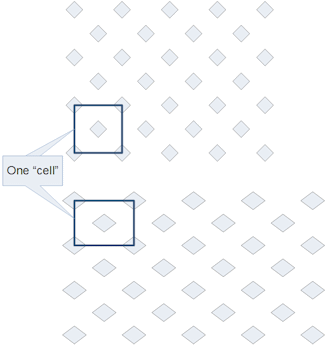This shows both a square (top) and 4/3 ratio (bottom) grid, highlighting one "cell".

2.

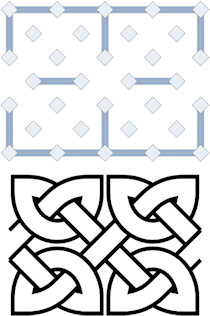This illustrates the basic 1-1 (square) ratio proportion, using a pattern from the Maiden Stone (also called "Double Stafford Knot").

3.

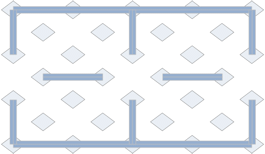Here is the 4/3 ratio grid with the same Maiden Stone pattern set up.

4.

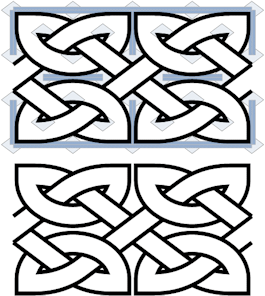Here is the template above with interlacing added. The bands are interlaced just as in the square grids, but you need to watch the band angles so they meet up with the grid guides. Using 4/3 ratio grids can help if you need to squeeze in a certain number of grid cells into a space that is not quite big enough and more square grids are not working either. The original Insular Celtic scribes used this technique in several instances; they even used odd (neither 1/1 nor 4/3) grid sizes to adjust border spacing.

1.

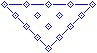This is the grid used for the knot.   (Please see the Basic Interlacing Construction page for information on the grid patterns used...) [BainI] would refer to this as a 4n grid--it uses four divisions across the long side of the triangle.  You should experiment with different amounts of cells across the long side.  The original artists used just enough cells to fit their pattern--a very tight grid.  Four is about as small as one can go...

2.

To build this simple pattern, first sketch in the corners of the triangle.  Size the bands as you would for the usual knotwork pattern--watch the width of the band that moves across the top of the triangle as it can be tricky to size properly.  

3.

This view shows how the corners are connected for this pattern.  Unlike with knotwork patterns (see the Basic Interlacing Construction page for details), I've always had to draw the band edges first and then erase the overlaps while interlacing. 

4.

After interlacing the bands show the common over-under pattern of all knotwork.  

5.

Finally, the bands are colored and the background darkened.  As with any knotwork pattern, the bands can be treated in a number of ways.  See the Line Treatments class page for details.  

1.

This view shows the pattern sketched in.  The "inside" corner pattern was changed to make the bands "flow" over and under rather than turn the corner as in Step 2 above.  

2.

Connect the corners and interlace, as in Step 4 above.  

3.

This shows the pattern repeated to form a square.  On the computer I simply copied, turned the copy 90 degrees, and pasted it back four times.  By hand, one duplicates the grid and interlaces each of the four separately.  Remember that the middle interlace drives the rest of the pattern, so do it first.  

4.

Finally, color in the band and background, or use another band treatment of your choice.  

1.

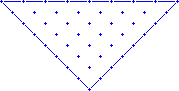The grid for this pattern is 8 cells wide across the top.

2.

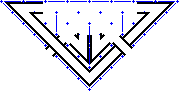The Dunfallandy pattern is more complex, so I've used "walls" to represent the places where bands split and curve.  This is similar to the techniques used in the Interrupted Interlacing class page.  I've also sketched in the corner bands.   In this pattern note that bands go "through" the sides of the triangle.

3.

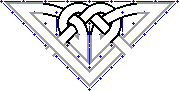As with the simple patterns, I've added the bands and interlaced.  With this more complex design, you can see how the interlacing is related to standard, square knotwork--over-then-under, the bands "turning" at walls and corners.  With wide bands like this, you need to really watch the width of the bands so they remain constant.  Things do get tight!

4.

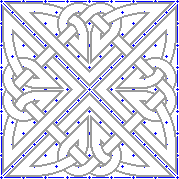As before, I copied and repeated the pattern in Step 3 with 90 degree turns to form the square found on the original stone.  Use the same techniques as in the simple panel above.

5.

This shows the bands and background colored in.

1.

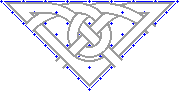This shows one fourth of the total Britford pattern.  This could be repeated and turned to form a square as with the Dunfallandy pattern used in the previous section.  

2.

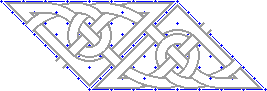In this view I've flipped the pattern over and connected it to the original.  It was fairly easy to do this, since the band connections lined up.  If they don't line up naturally, the pattern will have to be modified or shifted to make them connect.

3.

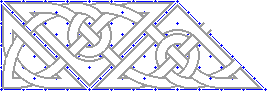For this border I had to put in a little place-holder knot to make it come out square on the end.  Should have worked harder on this, since it makes a "loop" in the pattern :-(  On some of the other triangular knotwork borders I put in a small zoomorphic "lizard" head and tail to complete the pattern.  Please see my Celtic "Art" pages for more examples.

4.

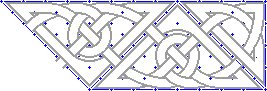I added a free-form knot on the other end as well...

5.

Starting with the pattern from step 3, I can add step 2 sections 'till the pattern gets as long as I need, then complete he border with a step 4 section.  The result is shown below:

6.

Finally, I colored in the bands and backgrounds.  As usual, you can use any band treatment desired.  The result using simple colored bands is shown below:

7.

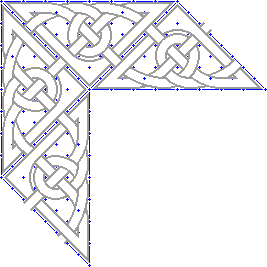Since the triangular patterns naturally turn 90 degrees, it is fairly easy to have a triangular knotwork border turn corners.  A pattern for the corner is shown here.  It can be combined (flipped and rotated as well) with patterns from steps 2-4 above to form a border of about any shape desired.  

1.

Determine the starting pattern. In this case we'll be using a pattern from the Book of Kells Folio 124R that (appropriately) was used in an annular area filling in an initial letter.

2.

Develop via analysis (or look up) the underlying interlace and cellular pattern (a 4X3 cell design in this case).

3.

Figure out how many cells you'll need. Let's say we want six repeats of the pattern around the whole annular area. Since the pattern we're using is four cells wide, we'll need 6 (repeats) x 4 (cell width) or 24 cells around the whole. So, each cell will be 360 (degrees in a circle) / 24 (cells around) or 15 degrees wide.

4.

Draw the initial grid. It really helps to have a computer drawing package to perform this step, let me tell you! It might take a few tries to get the cells about the right size. You will need to adjust the radius of the inner and outer boundaries of the annular region so that the cells you'll be drawing are fairly "square" (that is the top-bottom distance is about the same as the left-right distance. The following shows the whole annular grid for this pattern, showing the 15 degree cell spacing and highlighting a single annular cell:

5.

Now, add the cellular pattern walls and interruptions, repeating these six times around the circle:

6.

Interlace one of the six segments (we'll start at the top center for this example). The interlacing is done just like the linear knotwork we've done before, though you'll need to curve the bands to fit into the annular area to be covered.

7.

Finally, repeat the interlacing for the other five segments, using any band treatment desired: